Tag: clustering

Posted on in Machine Learning

Clustering Autoencoders: Comparing DEC and DCN

Deep autoencoders are a good way to learn representations and structure from unlabelled data. There are many variations, but the main idea is simple: the network consists of an encoder, which converts the input into a low-dimensional latent vector, and a decoder, which reconstructs the original input. Then, the latent vector captures the most essential information in the input.

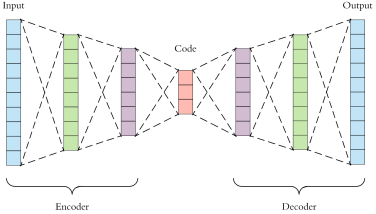
autoencoder

Above: Diagram of a simple autoencoder (Source)

One of the uses of autoencoders is to discover clusters of similar instances in an unlabelled dataset. In this post, we examine some ways of clustering with autoencoders. That is, we are given a dataset and K, the number of clusters, and need to find a low-dimensional representation that contains K clusters.

Problem with Naive Method

An naive and obvious solution is to take the autoencoder, and run K-means on the latent points generated by the encoder. The problem is that the autoencoder is only trained to reconstruct the input, with no constraints on the latent representation, and this may not produce a representation suitable for K-means clustering.

naive-failure

Above: Failure example with naive autoencoder clustering — K-means fails to find the appropriate clusters

Above is an example from one of my projects. The left diagram shows the hidden representation, and the four classes are generally well-separated. This representation is reasonable and the reconstruction error is low. However, when we run K-means (right), it fails spectacularly because the two latent dimensions are highly correlated.

Thus, our autoencoder can’t trivially be used for clustering. Fortunately, there’s been some research in clustering autoencoders; in this post, we study two main approaches: Deep Embedded Clustering (DEC), and Deep Clustering Network (DCN).

DEC: Deep Embedded Clustering

DEC was proposed by Xie et al. (2016), perhaps the first model to use deep autoencoders for clustering. The training consists of two stages. In the first stage, we initialize the autoencoder by training it the usual way, without clustering. In the second stage, we throw away the decoder, and refine the encoder to produce better clusters with a “cluster hardening” procedure.

dec-model

Above: Diagram of DEC model (Xie et al., 2016)

Let’s examine the second stage in more detail. After training the autoencoder, we run K-means on the hidden layer to get the initial centroids \{\mu_i\}_{i=1}^K. The assumption is the initial cluster assignments are mostly correct, but we can still refine them to be more distinct and separated.

First, we soft-assign each latent point z_i to the cluster centroids \{\mu_i\}_{i=1}^K using the Student’s t-distribution as a kernel:

q_{ij} = \frac{(1 + ||z_i - \mu_j||^2 / \alpha)^{-\frac{\alpha+1}{2}}}{\sum_{j'} (1 + ||z_i - \mu_{j'}||^2 / \alpha)^{-\frac{\alpha+1}{2}}}

In the paper, they fix \alpha=1 (the degrees of freedom), so the above can be simplified to:

q_{ij} = \frac{(1 + ||z_i - \mu_j||^2)^{-1}}{\sum_{j'} (1 + ||z_i - \mu_{j'}||^2)^{-1}}

Next, we define an auxiliary distribution P by:

p_{ij} = \frac{q_{ij}^2/f_j}{\sum_{j'} q_{ij'}^2 / f_{j'}}

where f_j = \sum_i q_{ij} is the soft cluster frequency of cluster j. Intuitively, squaring q_{ij} draws the probability distribution closer to the centroids.

p-and-q-distributions

Above: The auxiliary distribution P is derived from Q, but more concentrated around the centroids

Finally, we define the objective to minimize as the KL divergence between the soft assignment distribution Q and the auxiliary distribution P:

L = KL(P||Q) = \sum_i \sum_j p_{ij} \log \frac{p_{ij}}{q_{ij}}

Using standard backpropagation and stochastic gradient descent, we can train the encoder to produce latent points z_i to minimize the KL divergence L. We repeat this until the cluster assignments are stable.

DCN: Deep Clustering Network

DCN was proposed by Yang et al. (2017) at around the same time as DEC. Similar to DEC, it initializes the network by training the autoencoder to only reconstruct the input, and initialize K-means on the hidden representations. But unlike DEC, it then alternates between training the network and improving the clusters, using a joint loss function.

dcn-model

Above: Diagram of DCN model (Yang et al., 2017)

We define the optimization objective as a combination of reconstruction error (first term below) and clustering error (second term below). There’s a hyperparameter \lambda to balance the two terms:

dcn-loss

This function is complicated and difficult to optimize directly. Instead, we alternate between fixing the clusters while updating the network parameters, and fixing the network while updating the clusters. When we fix the clusters (centroid locations and point assignments), then the gradient of L with respect to the network parameters can be computed with backpropagation.

Next, when we fix the network parameters, we can update the cluster assignments and centroid locations. The paper uses a rolling average trick to update the centroids in an online manner, but I won’t go into the details here. The algorithm as presented in the paper looks like this:

dcn-algorithm

Comparisons and Further Reading

To recap, DEC and DCN are both models to perform unsupervised clustering using deep autoencoders. When evaluated on MNIST clustering, their accuracy scores are comparable. For both models, the scores depend a lot on initialization and hyperparameters, so it’s hard to say which is better.

One theoretical disadvantage of DEC is that in the cluster refinement phase, there is no longer any reconstruction loss to force the representation to remain reasonable. So the theoretical global optimum can be achieved trivially by mapping every input to the zero vector, but this does not happen in practice when using SGD for optimization.

Recently, there have been lots of innovations in deep learning for clustering, which I won’t be covering in this post; the review papers by Min et al. (2018) and Aljalbout et al. (2018) provide a good overview of the topic. Still, DEC and DCN are strong baselines for the clustering task, which newer models are compared against.

References

  1. Xie, Junyuan, Ross Girshick, and Ali Farhadi. “Unsupervised deep embedding for clustering analysis.” International conference on machine learning. 2016.
  2. Yang, Bo, et al. “Towards k-means-friendly spaces: Simultaneous deep learning and clustering.” Proceedings of the 34th International Conference on Machine Learning-Volume 70. JMLR. org, 2017.
  3. Min, Erxue, et al. “A survey of clustering with deep learning: From the perspective of network architecture.” IEEE Access 6 (2018): 39501-39514.
  4. Aljalbout, Elie, et al. “Clustering with deep learning: Taxonomy and new methods.” arXiv preprint arXiv:1801.07648 (2018).