Effectively self-studying over the Internet

The Internet is a great invention. Just about everything in humanity’s knowledge can be found on the Internet: with just a few keystrokes, you can find dozens of excellent quality textbooks, YouTube videos and blog posts about any topic you want to learn. The information is accessible to a degree that scholars and inventors could have hardly dreamed of even a few decades ago. With the popularity of remote work and everything moving online this decade, it is not surprising that many people are eager to learn new skills from the Internet.

However, despite the abundance of resources, self-studying over the Internet is harder than you think. You can easily find a list of resources on your topic, full of courses and textbooks to study from (like this one for theoretical physics). This knowledge is, in theory, enough to make you an expert, if only you were able to go through it all.

The problem is that internet self-study tends to be a passive activity. Humans cannot learn new skills effectively by only passively absorbing knowledge, we learn by doing. Ideally, 70% of your time should be active practice, trying to do the skill and learning from experience, and maybe 30% of the time on passively reading to expand your theoretical and background knowledge. You can’t learn to ski just by reading books and watching tutorials about it, at some point, you will need to actually put on a pair of skis and head to the mountains.

Some skills are relatively straightforward to actively practice using only a computer. Learning to program, for example: you can build a fully functional website with just a laptop and all the tools you need are available for free on the Internet. If you want to learn music production, everything can be done in software, and you need only a modest budget to buy some equipment. If you want to learning digital marketing, just set up an ecommerce website and play around with some Google ad campaigns, and you are good to go.

But many skills cannot be done using just a computer, in which case self-studying over the Internet is much more difficult. If you want to study chemistry, you can’t just set up a lab in your house and start playing around with chemicals. When the subject requires institutional resources to participate actively, this makes it difficult to self-study. In some cases it’s not even clear what counts as “actively” doing it, like studying philosophy or literature.

The situation is not hopeless, though. What you need to do is try to make it as an active process as possible. Here I will talk about some strategies I have used to learn more actively.

If possible, learn by doing it. Obvious, but worth reiterating one more time. Even for activities done on the computer, it is very tempting to passively consume content about it instead of actively practicing. Many music production students watch hours of tutorials about how to use various plugins and their features, instead of working on producing a song.

This is human nature, we are lazy creatures and passively consuming content is much easier than doing. It feels like we are learning something, but if we don’t put the knowledge to use, we’ll quickly forget it. If your skill requires some modest investment in tools and equipment to start doing, it is well worth it since you will learn much faster.

Do the exercises. Many textbooks and courses come with exercises to help you practice. In some fields, like mathematics, the standard way of learning is by doing lots of exercises. And in most university courses, much of your grade come from assignments that you hand in.

In practice, though, I’ve found it difficult to get enough motivation to do exercises properly, when I know that nobody is going to read it, and the experience is not very satisfying. Also, with nobody to check your answers, you don’t know if you did it incorrectly. But even a few exercises are better than not doing any at all, and anyhow the first few are the most valuable since you get diminishing returns the more exercises you do.

Discuss with others. The ideal situation is if you know somebody who is more experienced than you in the activity, then you can meet with them periodically to discuss what you are learning (and buy them a lunch for the favor). If you can find a friend who is not an expert but is interested in learning the same subject together, that is helpful as well. Even if they are at the same level as you, they’ll uncover some knowledge gaps that you missed and vice-versa.

Take online lessons. A hack that I’ve used on numerous occasions when I don’t know anybody who knows the topic I’m learning is buying an expert’s time via online lessons. For learning languages, I like Italki, a platform where you pay hourly for lessons with a native speaker. There are platforms where you can schedule lessons on a variety of topics, or buy consulting sessions with an expert.

The most effective way to use online lessons is to come prepared with a list of questions, or ask for feedback on something you attempted to do. In my Italki sessions, what I often do is write a passage of text in Spanish, and during the lesson, have my teacher correct it for mistakes in grammar and phrasing. It’s important to do this because otherwise, many teachers will simply regurgitate lesson material that they prepared in advance, which is no better than just watching a YouTube video.

Write blog posts. This is one of the best ways to actively learn and can be applied to any subject. It is effective because it will be visible to the public, so you will naturally make a serious effort to do it properly (much more than when doing throwaway exercises). I write blog post because I prefer the written medium; some people prefer to make YouTube videos which has a similar effect.

One limitation is that you can get it completely wrong, unwillingly spread misinformation, and nobody will notice or care enough to correct you. In other cases, readers have contacted me to correct errors on my blog post, which is helpful for improving the content (albeit not so helpful for my learning if it has been several years since I wrote it and I’ve already forgotten all the details).

Write book reviews. It is a lot of effort to write a blog post, and recently, not something that I’ve done that often. Instead, a lower effort version that I’ve been doing is writing a book review blog where I write a short summary and review of every book that I read. These are relatively quick to write since I’m just summarizing the main points of a book that I’ve just read (and is fresh on my mind), and I’m not trying to think of something original to say like for my blog posts, yet writing it is still somewhat of an active process.

How I write NLP papers in 8 months: idea to publication

Earlier this month I defended my PhD thesis. The bulk of the work of a PhD consists of producing peer-reviewed publications, and in my field, three first-author publications on a coherent topic in top-tier venues (EMNLP, ACL, NAACL, TACL, etc) is typically sufficient to earn a PhD.

Reflecting on my process for producing my three papers, I noticed that all of them took roughly 8-10 months from the time of the initial idea, until submitting the 8-page manuscript to a conference. Furthermore, each paper followed a similar trajectory from how it evolved from a vague idea into a concrete research contribution.

This is definitely not the only way to write papers, but it has worked well for me. All three of my papers were accepted into main conferences on the first attempt, with reviewer scores consistently between 3.5 and 4 (on a 1-5 rating scale). Therefore, I think it’s a good method to iterate on research projects and reliably produce strong NLP papers.

Month 1: Literature review

When I begin a project, I typically only have a vague idea of the direction or some phenomenon I want to explore. Since I don’t have a good understanding yet of the field, it helps to spend some time reading the prior literature at this stage, instead of diving into experiments right away. This is my focus for the first 3-4 weeks of a project.

See my blog post here for a guide on how to find and read research papers.

By the end of the first month, I would’ve read about 50 papers, and have a good understanding of:

• The theoretical frameworks and assumptions related to the problem.
• Recent work in this area, and what datasets and methodologies they use to solve it.
• Major challenges and open problems in this area, and why they remain difficult to solve.

At this point, after familiarizing myself with the recent work, I can usually identify some gaps that have not yet been addressed in the literature and have some ideas of how to begin solving them. This is when I begin running experiments – these initial experiments almost never make it into the final paper, but allow me to start building an intuition for the problem and become familiar with commonly used dataset and techniques.

Months 2-4: Exploration

The next phase of the project is iterative exploration and experimentation. For the next two or three months, I work on experiments, building on top of each other and using lessons learned from one experiment to guide the design of the next. Most of these experiments will be “failures” – inconclusive for various reasons:

• I discover that some theoretical assumptions turn out to be invalid, rendering the experiment pointless.
• After running the experiment, I find that the results are not very interesting: they are explainable by something obvious, or there are no consistent patterns.
• I try to run the experiment, but find that it’s impossible because the dataset is missing some crucial feature, or my tools are not powerful enough.

One thing you should never do is decide beforehand what evidence you want to find, and then run experiments until you find it. That would be bad science. So in this context, an experiment failure means it didn’t produce a result that’s interesting enough to include in a paper. An experiment might produce results that are different from what I expected, while being a very interesting and successful experiment.

During this phase, I read papers in a different way from the first month. Rather than casting a wide net, my reading is more focused on understanding details so that I can execute a specific experiment correctly.

After a few months of iteration and doing about 15-20 experiments, I have at least 2 or 3 with sufficiently interesting or cool results that I want to share with the community. These experiments will form the core of my new paper, but it’s not enough, since I still have to tie them together into a single coherent narrative, and strengthen all the weaknesses that would be mercilessly attacked during peer review.

Month 5: Telling a story

Before you can write a paper, you have to decide on a framing or narrative that aligns with your experiments. If this is not done correctly, the reader will be confused; your experiments will feel incoherent and unmotivated.

The same data and experiments can be framed in many different ways. Is our focus on evaluating several NLP models on how well they represent some linguistic property? Or are we using evidence from NLP models to argue for some theory of human language learnability? Or perhaps our main contribution is releasing a novel dataset and annotation schema?

To decide on a framing, we must consider several possible narratives and pick the one that best aligns holistically with our core experiments. We’ll need to provide a justification for it, which is usually not the original reason we did the experiment (since the exploration phase is so haphazard).

The product of this narrative brainstorming is a draft of an abstract of the final paper, containing the main results and motivation for them. By writing the abstract first, the overall scientific goal and structure of the paper is clarified. This also gives everyone an idea of gaps in the narrative and what experiments are still needed to fill in these gaps. Around this time is when I decide on a conference submission date to aim for, around 3-4 months down the road.

Months 6-7: Make it stronger

Now we are on the home stretch of the project: we have decided on the core contributions, we now just have to patiently take the time to make it as strong as possible. I make a list of experiments to be done to strengthen the result, like running it with different models, different datasets in other languages, ablation studies, controlling for potential confounding variables, etc.

Essentially I look at my own paper from the perspective of a reviewer, asking myself: “why would I reject this paper?” My co-authors will help out by pointing out flaws in my reasoning and methodology, anticipating problems in advance of the official peer review and giving me ample time to fix them. The paper probably has a decent chance of acceptance without all this extra work, but it is worth it because it lowers the risk of having the paper rejected and needing to resubmit, which would waste several valuable months for everyone.

Month 8: Paper writing

It takes me about 3 weeks to actually write the paper. I like to freeze all the code and experimental results one month before the deadline, so that during the last month, I can focus on presentation and writing. When all the tables and figures are in place, it is a lot easier to write the paper without having to worry about which parts will need to be updated when new results materialize.

The experiment methodology and results sections are the easiest to write since that’s what’s been on my mind for the past few months. The introduction is the most difficult since I have to take a step back and think about how to present the work for someone who is seeing it for the first time, but it is the first thing the reader sees and it’s perhaps the most important part of the whole paper.

A week before the deadline, I have a reasonably good first draft. After sending it out to my co-authors one last time to improve the final presentation, I’m ready to press the submit button. Now we cross our fingers and wait eagerly for the acceptance email!

Parting advice

There were two things that helped me tremendously during my PhD: reading lots of NLP papers, and having a good committee.

Reading a lot of NLP papers is really useful because it helps you build an intuition of what good and bad papers look like. Early in my research career, I participated in a lot of paper reading groups, where we discuss recent papers (both published and arXiV preprints) and talk about which parts are strong and weak, and why. I notice recurring trends of common problems and how strong papers manage them, so that I can incorporate the same solutions in my own papers.

This is sort of like training a GAN (generative adversarial network). I trained myself to be a good discriminator of good vs bad papers, and this is useful for my generator as well: when my paper passes my own discriminator, it is usually able to pass peer review as well.

Another thing that helped me was having a solid committee of experts from different academic backgrounds. This turned out to be very useful because they often pointed out weaknesses and faulty assumptions that I did not realize, even if they didn’t have a solution of how to fix these problems. This way I have no surprises when the peer reviews come out: all the weaknesses have already been pointed out.

For the PhD students reading this, I have two pieces of advice. First, read lots of papers to fine-tune your discriminator. Second, get feedback on your papers as often and as early as possible. It is a lot less painful at this stage when you’re still in the exploratory phase of the project, rather than after you’ve submitted the paper to get the same feedback from reviewers.

I am looking for a position as an NLP research scientist or machine learning engineer. Here is my CV. I can work in-person from Vancouver, Canada or remotely. If your company is hiring, please leave me a message!

Virtual NLP Conferences: The Good and the Bad

We are now almost two years into the COVID-19 pandemic: international travel has slowed to a trickle and all machine learning conferences have moved online. By now, most of my PhD research has taken place during the pandemic, which I’ve presented at four online conferences (ACL ’20, EMNLP ’20, NAACL ’21, and ACL ’21). I’ve also had the fortune to attend a few in-person conferences before the pandemic, so in this post I’ll compare the advantages of each format.

Travel

One of the perks of choosing grad school for me was the chance to travel to conferences to present my work. Typically the first author of each paper gets funded by the university to present their work. The university pays for the conference fees, hotels, and airfare, which adds up to several thousand dollars per conference. With all conferences online, the school only pays for the conference fee (a trivial amount, about $25-$100). Effectively, a major part of grad student compensation has been cut without replacing it with something else.

There are some advantages though. Before the pandemic, it was mandatory to travel to present your work at the conference. This can be at an inconvenient time or location (such as a 20-hour flight to Australia), so I avoided submitting to certain conferences because of this. With virtual conferences, I can submit anywhere without location being a factor.

Another factor is climate change. The IPCC report this year announced that the earth is warming up at an alarming rate, and at an individual level, one of the biggest contributors to greenhouse gas emissions is air travel. Thousands of grad students travelling internationally several times a year adds up to a significant amount of carbon emissions. Therefore, unless there are substantial benefits to meeting in-person, the climate impact alone is probably worth keeping to virtual conferences post-pandemic.

Talks and Posters

Typically in conferences, paper presentations can be oral (12-minute talk with 3 minutes Q/A), or poster (stand beside a poster for 2 hours). Online conferences mimiced the format: oral presentations were done in Zoom calls, while poster sessions were done in Gather Town (a game-like environment where you move around an avatar). Additionally, most conferences got the authors to record their presentations in advance, so the videos were available to watch at any time during the conference and afterwards.

Above: Presenting my poster in Gather Town (ACL 2021)

For me, Gather Town was quite successful at replicating the in-person conference discussion experience. I made a list of people I wanted to talk to, and either attended their poster session if they had one, otherwise logged on to Gather Town several times a day to check if they were online, and then go talk to them. This created an environment where it was easy to enter into spontaneous conversations, without the friction of scheduling a formal Zoom call with them.

The live oral sessions on Zoom were quite pointless, in my opinion, since the videos were already available to watch asynchronously at your own pace. There was no real opportunity for interaction in the 3-minute Q/A period, so this felt like a strictly worse format than just watching the videos (I usually watch these at 2x speed, which is impossible in a live session). Therefore I didn’t attend any of them.

The paper talk videos were by far the most useful feature of online conferences. Watching a 12-minute video is a good way of getting a high-level overview of a paper, and much faster than reading the paper: I typically watch 5 of them in one sitting. They are available after the conference, leaving a valuable resource for posterity. This is one thing we should keep even if we return to in-person conferences: the benefit is high, while the burden to authors is minimal (if they already prepared to give a talk, it is not much additional effort to record a video).

Collaborations

A commonly stated reason in favor of in-person conferences is the argument that face-to-face interaction is good for developing collaborations across universities. In my experience at in-person conferences, while I did talk to people from other universities, this never resulted in any collaborations with them. Other people’s experiences may vary though, if they’re more extroverted than me.

Virtual meetings certainly puts a strain on collaborations, but this makes more sense for collaborations within an institution. (For example, I haven’t talked to most people in my research group for the last year and a half, and have no idea what they’re working on until I see their paper published). This probably doesn’t extend to conferences though: one week is not enough time for any serious cross-institution collaboration to happen.

Final Thoughts

Like many others, I regret having missed out on so many conferences, which used to be a quintessential part of the PhD experience. There is a positive side: virtual conferences are a lot more accessible, making it feasible to attend conferences in adjacent research areas (like ICML, CVPR), since the $50 registration fee is trivial compared to the cost of travelling internationally.

Many aspects of virtual conferences have worked quite well, so we should consider keeping them virtual after the pandemic. The advantages of time, money, and carbon emissions are significant. However, organizers should embrace the virtual format and not try to mimic a physical conference. There is no good reason to have hours of back-to-back Zoom presentations, when the platform supports uploading videos to play back asynchronously. The virtual conference experience can only get better as organizers learn from past experience and the software continues to improve.

The Efficient Market Hypothesis in Research

A classic economics joke goes like this:

Two economists are walking down a road, when one of them notices a $20 bill on the ground. He turns to his friend and exclaims: “Look, a $20 bill!” The other replies: “Nah, if there’s a $20 on the bill on the ground, someone would’ve picked it up already.”

The economists in the joke believe in the Efficient Market Hypothesis (EMH), which roughly says that financial markets are efficient and there’s no way to “beat the market” by making intelligent trades.

If the EMH was true, then why is there still a trillion-dollar finance industry with active mutual funds and hedge funds? In reality, the EMH is not a universal law of economics (like the law of gravity), but more like an approximation. There may exist inefficiencies in markets where stock prices follow a predictable pattern and there is profit to be made (e.g.: stock prices fall when it’s cloudy in New York). However, as soon as someone notices the pattern and starts exploiting it (by making a trading algorithm based on weather data), the inefficiency disappears. The next person will find zero correlation between weather in New York and stock prices.

There is a close parallel in academic research. Here, the “market” is generally efficient: most problems that are solvable are already solved. There are still “inefficiencies”: open problems that can be reasonably solved, and one “exploits” them by solving it and publishing a paper. Once exploited, it is no longer available: nobody else can publish the same paper solving the same problem.

Where does this leave the EMH? In my view, the EMH is a useful approximation, but its accuracy depends on your skill and expertise. For non-experts, the EMH is pretty much universally true: it’s unlikely that you’ve found an inefficiency that everyone else has missed. For experts, the EMH is less often true: when you’re working in highly specialized areas that only a handful of people understand, you begin to notice more inefficiencies that are still unexploited.

A large inefficiency is like a $20 bill on the ground: it gets picked up very quickly. An example of this is when a new tool is invented that can straightforwardly be applied to a wide range of problems. When the BERT model was released in 2018, breaking the state-of-the-art on all the NLP benchmarks, there was instantly an explosion of activity as researchers raced to apply it to all the important NLP problems and be the first to publish. By mid-2019, all the straightforward applications of BERT were done, and the $20 bill was no more.

Above: Representation of the EMH in research. To outsiders, there are no inefficiencies; to experts, inefficiencies exist briefly before they are exploited. Loosely inspired by this diagram by Matt Might.

The EMH implies various heuristics that I use to guide my daily research. If I have a research idea that’s relatively obvious, and the tools to attack it have existed for a while (say, >= 3 years), then probably one of the following is true:

1. Someone already published it 3 years ago.
2. Your idea doesn’t work very well.
3. The result is not that useful or interesting.
4. One of your basic assumptions is wrong, so your idea doesn’t even make sense.
5. Etc.

Conversely, a research idea is much more likely to be fruitful (i.e., a true inefficiency) if the tools to solve it have only existed for a few months, requires data and resources that nobody else has access to, or requires rare combinations of insights that conceivably nobody has thought of.

Outside the realm of the known (the red area in my diagram), there are many questions that are unanswerable. These include the hard problems of consciousness and free will, P=NP, etc, or more mundane problems where our current methods are not strong enough. For an outsider, these might seem like inefficiencies, but it would be wise to assume they’re not. The EMH ensures that true inefficiencies are quickly picked up.

To give a more relatable example, take the apps Uber (launched in 2009) and Instagram (launched in 2010). Many of the apps on your phone probably launched around the same time. In order for Uber and Instagram to work, people needed to have smartphones that were connected to the internet, with GPS (for Uber) and decent quality cameras (for Instagram). Neither of these ideas would’ve been possible in 2005, but thanks to the EMH, as soon as smartphone adoption took off, we didn’t have to wait very long to see all the viable use-cases for the new technology to emerge.

What if the government hadn’t released any Coronavirus economic stimulus?

It is March 23, 2020. After a month of testing fiascos, COVID-19 is ravaging the United States, with 40,000 cases in the US and 360,000 worldwide. There is a growing sense of panic as cities begin to lock down. Market circuit breakers have triggered four times in quick succession, with the stock market losing 30% of its value in mere weeks. There’s no sign that the worst is over.

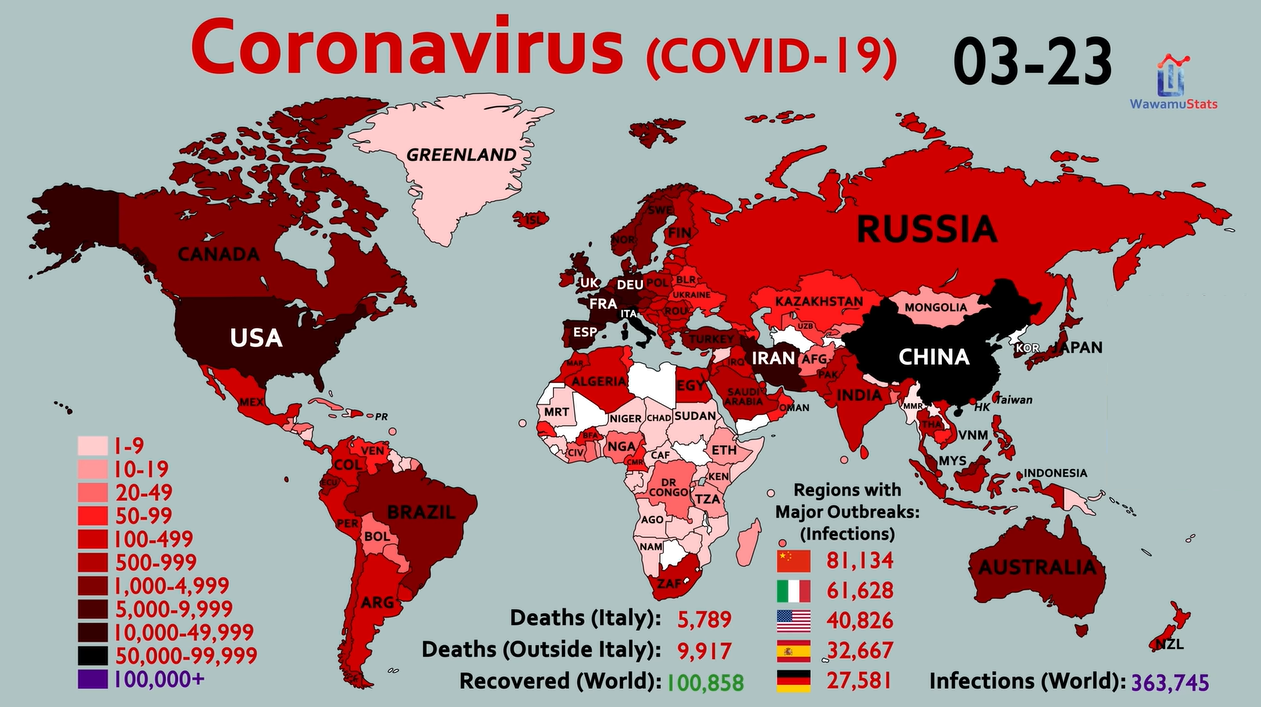Above: Global Coronavirus stats on March 23, 2020, when the S&P 500 reached its lowest point during the pandemic (Source).

With businesses across the country closed and millions out of work, it’s clear that a massive financial stimulus is needed to prevent a total economic collapse. However, Congress is divided and is unable to pass the bill. Even when urgent action is needed, they squabble and debate over minor details, refusing to come to a compromise. The president denies that there’s any need for action. Both the democrats and the republicans are willing to do anything to prevent the other side from scoring a victory. The government is in a gridlock.

Let the businesses fail, they say. Don’t bail them out, they took the risk when the times were good, now you reap what you sow. Let them go bankrupt, punish the executives taking millions of dollars of bonuses. Let the free market do its job, after all, they can always start new businesses once this is all over.

April comes without any help from the government. Massive layoffs across all sectors of the economy as companies see their revenues drop to a fraction of normal levels, and layoff employees to try to preserve their cash. Retail and travel sectors are the most heavily affected, but soon, all companies are affected since people are hesitant to spend money. Unemployment numbers skyrocket to levels even greater than during the Great Depression.

Without a job, millions of people miss their rent payments, instead saving their money for food and essential items. Restaurants and other small businesses shut down. When people and businesses cannot pay rent, their landlords cannot pay the mortgages that they owe to the bank. A few small banks go bankrupt, and Wall Street waits anxiously for a government bailout. But unlike 2008, the state is in a deadlock, and there is no bailout coming. In 2020, no bank is too big to fail.

Each bank that goes down takes another bank down with it, until there is soon a cascading domino effect of bank failures. Everyone rushes to withdraw cash from their checking accounts before the bank collapses, which of course makes matters worse. Those too late to withdraw their cash lose their savings. This is devastation for businesses: even for those that escaped the pandemic, but there is no escaping systemic bank failure. Companies have no money in the bank to pay suppliers or make payroll, and thus, thousands of companies go bankrupt overnight.

Across the nation, people are angry at the government’s inaction, and take to the streets in protest. Having depleted their savings, some rob and steal from grocery stores to avoid starvation. The government finally steps in and deploys the military to keep order in the cities. They arrange for emergency supplies, enough to keep everybody fed, but just barely.

The lockdown lasts a few more months, and the virus is finally under control. Everyone is free to go back to work, but the problem is there are no jobs to go back to. In the process of all the biggest corporations going bankrupt, society has lost its complex network of dependencies and organizational knowledge. It only takes a day to lay off 100,000 employees, but to build up this structure from scratch will take decades.

A new president is elected, but it is too late, the damage has been done and cannot be reversed. The economy slowly recovers, but with less efficiency than before, and with workers employed in less productive roles, and the loss of productivity means that everyone enjoys a lower standard of living. Five years later, the virus is long gone, but the economy is nowhere close to its original state. By then, China emerges as the new dominant world power. The year 2020 goes down in history as a year of failure, where through inaction, a temporary health crisis led to societal collapse.

---

In our present timeline, fortunately, none of the above actually happened. The democrats and republicans put aside their differences and on March 25, swiftly passed a $2 billion dollar economic stimulus. The stock market immediately rebounded.

There was a period in March when it was seemed the government was in gridlock, and it wasn’t clear whether the US was politically capable of passing such a large stimulus bill. Is an economic collapse likely? Not really — no reasonable government would have allowed all of the banks to fail, so we would likely have a recession and not a total collapse. Banks did fail during the Great Depression, but macroeconomic theory was in its infancy at that time, and there’s no way such mistakes would’ve been repeated today. Still, this is the closest we’ve come to an economic collapse in a long time, and it’s fun to speculate about the consequences of what it would be like.

Predictions for 2030

Now that it’s Jan 1, 2020, I’m going to make some predictions about what we will see in the next decade. By the year 2030:

• Deep learning will be a standard tool and integrated into workflows of many professions, eg: code completion for programmers, note taking during meetings. Speech recognition will surpass human accuracy. Machine translation will still be inferior to human professionals.

• Open-domain conversational dialogue (aka the Turing Test) will be on par with an average human, using a combination of deep learning and some new technique not available today. It will be regarded as more of a “trick” than strong AI; the bar for true AGI will be shifted higher.

• Driverless cars will be in commercial use in a few limited scenarios. Most cars will have some autonomous features, but full autonomy still not widely deployed.

• S&P 500 index (a measure of the US economy, currently at 3230) will double to between 6000-7000. Bitcoin will still exist but its price will fall under 1000 USD (currently ~7000 USD).

• Real estate prices in Toronto will either have a sharp fall or flatten out; overall increase in 2020-2030 period will not exceed inflation.

• All western nations will have implemented some kind of carbon tax as political pressure increases from young people; no serious politician will suggest removing carbon tax.

• About half of my Waterloo cohort will be married, but majority will not have any kids, at the age of 35.

• China will overtake USA as world’s biggest economy, but growth will slow down, and PPP per capita will still be well below USA.

Non-technical challenges of medical NLP research

Machine learning has recently made a lot of headlines in healthcare applications, like identifying tumors from images, or technology for personalized treatment. In this post, I describe my experiences as a healthcare ML researcher: the difficulties in doing research in this field, as well as reasons for optimism.

My research group focuses on applications of NLP to healthcare. For a year or two, I was involved in a number of projects in this area (specifically, detecting dementia through speech). From my own projects and from talking to others in my research group, I noticed that a few recurring difficulties frequently came up in healthcare NLP research — things that rarely occurred in other branches of ML. These are non-technical challenges that take up time and impede progress, and generally considered not very interesting to solve. I’ll give some examples of what I mean.

Collecting datasets is hard. Any time you want to do anything involving patient data, you have to undergo a lengthy ethics approval process. Even with something as innocent as an anonymous online questionnaire, there is a mandatory review by an ethics board before the experiment is allowed to proceed. As a result, most datasets in healthcare ML are small: a few dozen patient samples is common, and you’re lucky to have more than a hundred samples to work with. This is tiny compared to other areas of ML where you can easily find thousands of samples.

In my master’s research project, where I studied dementia detection from speech, the largest available corpus had about 300 patients, and other corpora had less than 100. This constrained the types of experiments that were possible. Prior work in this area used a lot of feature engineering approaches, because it was commonly believed that you needed at least a few thousand examples to do deep learning. With less data than that, deep learning would just learn to overfit.

Even after the data has been collected, it is difficult to share with others. This is again due to the conservative ethics processes required to share data. Data transfer agreements need to be reviewed and signed, and in some cases, data must remain physically on servers in a particular hospital. Researchers rarely open-source their code along with the paper, since there’s no point of doing so without giving access to the data; this makes it hard to reproduce any experimental results.

Medical data is messy. Data access issues aside, healthcare NLP has some of the messiest datasets in machine learning. Many datasets in ML are carefully constructed and annotated for the purpose of research, but this is not the case for medical data. Instead, data comes from real patients and hospitals, which are full of shorthand abbreviations of medical terms written by doctors, which mean different things depending on context. Unsurprisingly, many NLP techniques fail to work. Missing values and otherwise unreliable data are common, so a lot of not-so-glamorous data preprocessing is often needed.

---

I’ve so far painted a bleak picture of medical NLP, but I don’t want to give off such a negative image of my field. In the second part of this post, I give some counter-arguments to the above points as well as some of the positive aspects of research.

On difficulties in data access. There are good reasons for caution — patient data is sensitive and real people can be harmed if the data falls into the wrong hands. Even after removing personally identifiable information, there’s still a risk of a malicious actor deanonymizing the data and extracting information that’s not intended to be made public.

The situation is improving though. The community recognizes the need to share clinical data, to strike a balance between protecting patient privacy and allowing research. There have been efforts like the relatively open MIMIC critical care database to promote more collaborative research.

On small / messy datasets. With every challenge, there comes an opportunity. In fact, my own master’s research was driven by lack of data. I was trying to extend dementia detection to Chinese, but there wasn’t much data available. So I proposed a way to transfer knowledge from the much larger English dataset to Chinese, and got a conference paper and a master’s thesis from it. If it wasn’t for lack of data, then you could’ve just taken the existing algorithm and applied it to Chinese, which wouldn’t be as interesting.

Also, deep learning in NLP has recently gotten a lot better at learning from small datasets. Other research groups have had some success on the same dementia detection task using deep learning. With new papers every week on few-shot learning, one-shot learning, transfer learning, etc, small datasets may not be too much of a limitation.

Same applies to messy data, missing values, label leakage, etc. I’ll refer to this survey paper for the details, but the take-away is that these shouldn’t be thought of as barriers, but as opportunities to make a research contribution.

In summary, as a healthcare NLP researcher, you have to deal with difficulties that other machine learning researchers don’t have. However, you also have the unique opportunity to use your abilities to help sick and vulnerable people. For many people, this is an important consideration — if this is something you care deeply about, then maybe medical NLP research is right for you.

Thanks to Elaine Y. and Chloe P. for their comments on drafts of this post.

NAACL 2019, my first conference talk, and general impressions

Last week, I attended my first NLP conference, NAACL, which was held in Minneapolis. My paper was selected for a short talk of 12 minutes in length, plus 3 minutes for questions. I presented my research on dementia detection in Mandarin Chinese, which I did during my master’s.

Here’s a video of my talk:

Visiting Minneapolis

Going to conferences is a good way as a grad student to travel for free. Some of my friends balked at the idea of going to Minneapolis rather than somewhere more “interesting”. However, I had never been there before, and in the summer, Minneapolis was quite nice.

Minneapolis is very flat and good for biking — you can rent a bike for $2 per 30 minutes. I took the light rail to Minnehaha falls (above) and biked along the Mississippi river to the city center. The downside is that compared to Toronto, the food choices are quite limited. The majority of restaurants serve American food (burgers, sandwiches, pasta, etc).

Meeting people

It’s often said that most of the value of a conference happens in the hallways, not in the scheduled talks (which you can often find on YouTube for free). For me, this was a good opportunity to finally meet some of my previous collaborators in person. Previously, we had only communicated via Skype and email. I also ran into people whose names I recognize from reading their papers, but had never seen in person.

Despite all the advances in video conferencing technology, nothing beats face-to-face interaction over lunch. There’s a reason why businesses spend so much money to send employees abroad to conduct their meetings.

Talks and posters

The accepted papers were split roughly 50-50 into talks and poster presentations. I preferred the poster format, because you get to have a 1-on-1 discussion with the author about their work, and ask clarifying questions.

Talks were a mixed bag — some were great, but for many it was difficult to make sense of anything. The most common problem was that speakers tended to dive into complex technical details, and lost sense of the “big picture”. The better talks spent a good chunk of time covering the background and motivation, with lots of examples, before describing their own contribution.

It’s difficult to make a coherent talk in only 12 minutes. A research paper is inherently a very narrow and focused contribution, while the audience come from all areas of NLP, and have probably never seen your problem before. The organizers tried to group talks into related topics like “Speech” or “Multilingual NLP”, but even then, the subfields of NLP are so diverse that two random papers had very little in common.

Research trends in NLP

Academia has a notorious reputation for inventing impractically complex models to squeeze out a 0.2% improvement on a benchmark. This may be true in some areas of ML, but it certainly wasn’t the case here. There was a lot of variety in the problems people were solving. Many papers worked with new datasets, and even those using existing datasets often proposed new tasks that weren’t considered before.

A lot of papers used similar model architectures, like some sort of Bi-LSTM with attention, perhaps with a CRF on top. None of it is directly comparable to one another because everybody is solving a different problem. I guess it shows the flexibility of Bi-LSTMs to be so widely applicable. For me, the papers that did something different (like applying quantum physics to NLP) really stood out.

Interestingly, many papers did experiments with BERT, which was presented at this conference! Last October, the BERT paper bypassed the usual conventions and announced their results without peer review, so the NLP community knew about it for a long time, but only now it’s officially presented at a conference.

Why Time Management in Grad School is Difficult

Graduate students are often stressed and overworked; a recent Nature report states that grad students are six times more likely to suffer from depression than the general population. Although there are many factors contributing to this, I suspect that a lot of it has to do with poor time management.

In this post, I will describe why time management in grad school is particularly difficult, and some strategies that I’ve found helpful as a grad student.

---

As a grad student, I’ve found time management to be far more difficult than either during my undergraduate years as well as working in the industry. Here are a few reasons why:

1. Loose supervision: as a grad student, you have a lot of freedom over how you spend your time. There are no set hours, and you can go a week or more without talking to your adviser. This can be both a blessing and a curse: some find the freedom liberating while others struggle to be productive. In contrast, in an industry job, you’re expected to report to daily standup, you get assigned tickets each sprint, so others essentially manage your time for you.
2. Few deadlines: grad school is different from undergrad in that you have a handful of “big” deadlines a year (eg: conference submission dates, major project due dates), whereas in undergrad, the deadlines (eg: assignments, midterms) are smaller and more frequent.
3. Sparse rewards: most of your experiments will fail. That’s the nature of research — if you know it’s going to work, then it’s no longer research. It’s hard to not get discouraged when you struggle for weeks without getting a positive result, and start procrastinating on a multitude of distractions.

Basically, poor time management leads to procrastination, stress, burnout, and generally having a bad time in grad school 😦

---

Some time management strategies that I’ve found to be useful:

1. Track your time. When I first started doing this, I was surprised at how much time I spent doing random, half-productive stuff not really related to my goals. It’s up to you how to do this — I keep a bunch of Excel spreadsheets, but some people use software like Asana.
2. Know your plan. My adviser suggested a hierarchical format with a long-term research agenda, medium-term goals (eg: submit a paper to ICML), and short-term tasks (eg: run X baseline on dataset Y). Then you know if you’re progressing towards your goals or merely doing stuff tangential to it.
3. Focus on the process, not the reward. It’s tempting to celebrate when your paper gets accepted — but the flip side is you’re going to be depressed if it gets rejected. Your research will have have many failures: paper rejections and experiments that somehow don’t work. Instead, celebrate when you finish the first draft of your paper; reward yourself when you finish implementing an algorithm, even if it fails to beat the baseline.

---

Here, I plotted my productive time allocation in the last 6 months:

Most interestingly, only a quarter of my time is spent coding or running experiments, which seems to be much less than most grad students. I read a lot of papers to try to avoid reinventing things that others have already done.

On average, I spend about 6 hours a day doing productive work (including weekends) — a quite reasonable workload of about 40-45 hours a week. Contrary to some perceptions, grad students don’t have to be stressed and overworked to be successful; allowing time for leisure and social activities is crucial in the long run.

Deep Learning for NLP: SpaCy vs PyTorch vs AllenNLP

Deep neural networks have become really popular nowadays, producing state-of-the-art results in many areas of NLP, like sentiment analysis, text summarization, question answering, and more. In this blog post, we compare three popular NLP deep learning frameworks: SpaCy, PyTorch, and AllenNLP: what are their advantages, disadvantages, and use cases.

SpaCy

Pros: easy to use, very fast, ready for production

Cons: not customizable, internals are opaque

SpaCy is a mature and batteries-included framework that comes with prebuilt models for common NLP tasks like classification, named entity recognition, and part-of-speech tagging. It’s very easy to train a model with your data: all the gritty details like tokenization and word embeddings are handled for you. SpaCy is written in Cython which makes it faster than a pure Python implementation, so it’s ideal for production.

The design philosophy is the user should only worry about the task at hand, and not the underlying details. If a newer and more accurate model comes along, SpaCy can update itself to use the improved model, and the user doesn’t need to change anything. This is good for getting a model up and running quickly, but leaves little room for a NLP practitioner to customize the model if the task doesn’t exactly match one of SpaCy’s prebuilt models. For example, you can’t build a classifier that takes both text, numerical, and image data at the same time to produce a classification.

PyTorch

Pros: very customizable, widely used in deep learning research

Cons: fewer NLP abstractions, not optimized for speed

PyTorch is a deep learning framework by Facebook, popular among researchers for all kinds of DL models, like image classifiers or deep reinforcement learning or GANs. It uses a clear and flexible design where the model architecture is defined with straightforward Python code (rather than TensorFlow’s computational graph design).

NLP-specific functionality, like tokenization and managing word embeddings, are available in torchtext. However, PyTorch is a general purpose deep learning framework and has relatively few NLP abstractions compared to SpaCy and AllenNLP, which are designed for NLP.

AllenNLP

Pros: excellent NLP functionality, designed for quick prototyping

Cons: not yet mature, not optimized for speed

AllenNLP is built on top of PyTorch, designed for rapid prototyping NLP models for research purposes. It supports a lot of NLP functionality out-of-the-box, like text preprocessing and character embeddings, and abstracts away the training loop (whereas in PyTorch you have to write the training loop yourself). Currently, AllenNLP is not yet at a 1.0 stable release, but looks very promising.

Unlike PyTorch, AllenNLP’s design decouples what a model “does” from the architectural details of “how” it’s done. For example, a Seq2VecEncoder is any component that takes a sequence of vectors and outputs a single vector. You can use GloVe embeddings and average them, or you can use an LSTM, or you can put in a CNN. All of these are Seq2VecEncoders so you can swap them out without affecting the model logic.

The talk “Writing code for NLP Research” presented at EMNLP 2018 gives a good overview of AllenNLP’s design philosophy and its differences from PyTorch.

Which is the best framework?

It depends on how much you care about flexibility, ease of use, and performance.

• If your task is fairly standard, then SpaCy is the easiest to get up and running. You can train a model using a small amount of code, you don’t have to think about whether to use a CNN or RNN, and the API is clearly documented. It’s also well optimized to deploy to production.
• AllenNLP is the best for research prototyping. It supports all the bells and whistles that you’d include in your next research paper, and encourages you to follow the best practices by design. Its functionality is a superset of PyTorch’s, so I’d recommend AllenNLP over PyTorch for all NLP applications.

There’s a few runner-ups that I will mention briefly:

• NLTK / Stanford CoreNLP / Gensim are popular libraries for NLP. They’re good libraries, but they don’t do deep learning, so they can’t be directly compared here.
• Tensorflow / Keras are also popular for research, especially for Google projects. Tensorflow is the only framework supported by Google’s TPUs, and it also has better multi-GPU support than PyTorch. However, multi-GPU setups are relatively uncommon in NLP, and furthermore, its computational graph model is harder to debug than PyTorch’s model, so I don’t recommend it for NLP.
• PyText is a new framework by Facebook, also built on top of PyTorch. It defines a network using pre-built modules (similar to Keras) and supports exporting models to Caffe to be faster in production. However, it’s very new (only released earlier this month) and I haven’t worked with it myself to form an opinion about it yet.

That’s all, let me know if there’s any that I’ve missed!